general
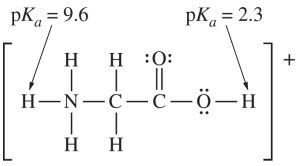 Which of the following is true about the geometry of the glycinium cation?( )
Which of the following is true about the geometry of the glycinium cation?( )
To solve the problem regarding the geometry of the glycinium cation, let&
039;s analyze each option:
Step 1: Analyze Option A
- The leftmost carbon atom is bonded to four atoms (three hydrogens and one nitrogen).- It has no nonbonding electron pairs, resulting in four electron domains.
- According to VSEPR theory, this leads to a tetrahedral geometry, not planar.
Step 2: Analyze Option B
- The central carbon atom is bonded to two oxygen atoms and one other carbon atom.- It has no nonbonding electron pairs, resulting in three electron domains.
- This configuration leads to a trigonal planar geometry (sp² hybridization), meaning all four atoms (two carbons and two oxygens) lie in the same plane.
Step 3: Analyze Option C
- The N-C-C bond angle is determined by the geometry around the carbon atoms.- The leftmost carbon is tetrahedral, leading to bond angles of approximately $$109^\circ$$, not $$180^\circ$$.
Step 4: Analyze Option D
- The nitrogen atom is bonded to four atoms (three hydrogens and one carbon).- It has no nonbonding electron pairs, resulting in four electron domains.
- This leads to a tetrahedral geometry, not planar.
Step 5: Conclusion
- Based on the analysis, Option B is correct: Both carbon atoms and both oxygen atoms lie in the same plane due to the trigonal planar geometry around the central carbon atom.Final Answer
- B: Both $$\mathrm{C}$$ atoms and both $$\mathrm{O}$$ atoms lie in the same plane. What is the approximate $$\mathrm{H}-\mathrm{O}-\mathrm{C}$$ bond angle in the glycinium cation?( )
What is the approximate $$\mathrm{H}-\mathrm{O}-\mathrm{C}$$ bond angle in the glycinium cation?( )
To determine the approximate $$\mathrm{H}-\mathrm{O}-\mathrm{C}$$ bond angle in the glycinium cation, we need to consider the geometry around the oxygen atom.
Step 1: Identify the Geometry
The oxygen atom in the $$\mathrm{H}-\mathrm{O}-\mathrm{C}$$ bond has two lone pairs of electrons.This results in a tetrahedral electron domain geometry.
Step 2: Understand Tetrahedral Geometry
In a perfect tetrahedral geometry, the bond angles are approximately $$109.5^\circ$$.However, lone pairs repel more strongly than bonding pairs, slightly reducing the bond angle.
Step 3: Consider the Effect of Lone Pairs
The presence of two lone pairs on the oxygen atom will compress the $$\mathrm{H}-\mathrm{O}-\mathrm{C}$$ bond angle slightly from the ideal tetrahedral angle.Step 4: Estimate the Bond Angle
Due to the repulsion from the lone pairs, the bond angle is slightly less than $$109.5^\circ$$, but still close to it.Step 5: Conclusion
The approximate $$\mathrm{H}-\mathrm{O}-\mathrm{C}$$ bond angle in the glycinium cation is close to $$109^\circ$$.Final Answer
The correct answer is C.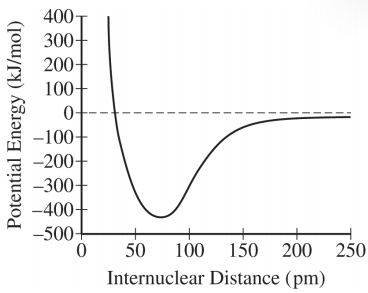

To solve this problem, we need to analyze the potential energy curve and its implications for the bond formation between two atoms.
Step 1: Understand the Potential Energy Curve
The curve shows the potential energy as a function of the internuclear distance between two atoms.The point where the potential energy is at its minimum indicates the most stable bond length.
Step 2: Identify the Minimum Potential Energy
From the graph, the minimum potential energy occurs around an internuclear distance of approximately 75 pm.This is the point where the system is most stable.
Step 3: Analyze the Forces at Different Distances
- At distances less than 75 pm, the potential energy increases sharply, indicating repulsive forces dominate.- At distances greater than 75 pm, the potential energy gradually increases, indicating attractive forces are present.
Step 4: Determine the Bond Length
The bond length corresponds to the internuclear distance at the minimum potential energy.Therefore, the bond length is 75 pm.
Step 5: Evaluate the Options
- Option A: Incorrect.At 25 pm, the force is repulsive, not forming a bond.
- Option B: Correct.
The bond forms at 75 pm, where the potential energy is minimum.
- Option C: Incorrect.
At 25 pm, the force is repulsive.
- Option D: Incorrect.
At 75 pm, the net force is zero, indicating a stable bond, not an attractive force.
Step 6: Conclusion
The correct inference from the diagram is that the atoms form a bond with a bond length of 75 pm.Thus, the answer is B.
Step 1. Understand the Problem Statement
The problem states that for all natural numbers $$n \geqslant 1$$, the inequality $$0 < b_n < a_n$$ holds.
We need to determine which statement must be true based on this inequality.
Step 2. Analyze the Given Inequality
The inequality $$0 < b_n < a_n$$ implies that both sequences $$b_n$$ and $$a_n$$ are positive for all $$n$$.
Additionally, $$b_n$$ is always less than $$a_n$$.
Step 3. Consider Possible Statements
To solve the problem, we need to consider possible statements about the sequences $$a_n$$ and $$b_n$$.
These could include statements about their limits, convergence, or divergence.
Step 4. Explore Convergence and Divergence
Since the problem does not provide specific sequences, we need to consider general properties of sequences.
One common property to explore is whether the sequences converge or diverge.
Step 5. Evaluate Limits
If both sequences converge, then their limits must satisfy the inequality $$0 < \lim_{n \to \infty} b_n \leq \lim_{n \to \infty} a_n$$.
If $$b_n$$ converges to a limit, say $$L_b$$, and $$a_n$$ converges to a limit, say $$L_a$$, then it must be true that $$L_b \leq L_a$$.
Step 6. Consider Special Cases
Consider the case where both sequences converge to the same limit.
In this case, $$L_b = L_a$$, which satisfies the inequality.
However, if $$b_n$$ diverges or converges to a different limit than $$a_n$$, the inequality still holds as long as $$L_b \leq L_a$$.
Step 7. Conclusion
The statement that must be true is that the limit of $$b_n$$ is less than or equal to the limit of $$a_n$$ if both limits exist.
This is a general property of sequences where one is always less than the other.
Therefore, the correct answer is B.
To solve the problem of finding the sum of the infinite series $$\sum_{k=1}^{\infty} a_k$$ given that the $$n$$th partial sum is $$S_n = (-1)^{n+1}$$ for $$n \geqslant 1$$, consider the following key points:
1. Partial Sum Definition: The partial sum $$S_n$$ is the sum of the first $$n$$ terms of the series, i.e., $$S_n = a_1 + a_2 + \cdots + a_n$$.
2. Behavior of Partial Sums: The given partial sum alternates between 1 and -1 as $$n$$ increases.
Specifically, for odd $$n$$, $$S_n = 1$$, and for even $$n$$, $$S_n = -1$$.
3. Convergence of Series: For an infinite series to converge to a sum, the sequence of partial sums must approach a finite limit as $$n$$ approaches infinity.
4. Analysis of Alternating Partial Sums: Since the partial sums alternate between 1 and -1, they do not approach a single finite limit.
This indicates that the series does not converge to a specific sum.
By understanding these points, you can determine the behavior of the series and its convergence properties.








