simple harmonic oscillations
Difficulty Levels:
1
Q&A
Medium
The defining equation of simple harmonic motion is
$$
a=-\omega^{2} x
$$
State the significance of the minus $$(-)$$ sign in the equation．
Answer:
acceleration and displacement are in opposite directions
Explanation:
2
Q&A
Medium
A trolley rests on a bench．Two identical stretched springs are attached to the trolley as shown in Fig．4．1．The other end of each spring is attached to a fixed support．
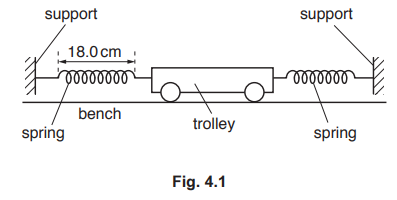The unstretched length of each spring is $$12.0 \mathrm{~cm}$$．The spring constant of each spring is $$8.0 \mathrm{Nm}^{-1}$$．When the trolley is in equilibrium the length of each spring is $$18.0 \mathrm{~cm}$$．
The trolley is displaced $$4.8 \mathrm{~cm}$$ to one side and then released．Assume that resistive forces on the trolley are negligible．
（i）Show that the resultant force on the trolley at the moment of release is $$0.77 \mathrm{~N}$$．
（ii）The mass of the trolley is $$250 \mathrm{~g}$$．
Calculate the maximum acceleration a of the trolley．
$$a=$$ $$\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots $$ $$\mathrm{m} \mathrm{s}^{-2}$$ [1]
（iii）Use your answer in（ii）to determine the period $$T$$ of the subsequent oscillation．
$$T=$$ $$\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots s$$ [3]
（iv）The experiment is repeated with an initial displacement of the trolley of $$2.4 \mathrm{~cm}$$．
State and explain the effect，if any，this change has on the period of the oscillation of the trolley．
The unstretched length of each spring is $$12.0 \mathrm{~cm}$$．The spring constant of each spring is $$8.0 \mathrm{Nm}^{-1}$$．When the trolley is in equilibrium the length of each spring is $$18.0 \mathrm{~cm}$$．
The trolley is displaced $$4.8 \mathrm{~cm}$$ to one side and then released．Assume that resistive forces on the trolley are negligible．
（i）Show that the resultant force on the trolley at the moment of release is $$0.77 \mathrm{~N}$$．
（ii）The mass of the trolley is $$250 \mathrm{~g}$$．
Calculate the maximum acceleration a of the trolley．
$$a=$$ $$\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots $$ $$\mathrm{m} \mathrm{s}^{-2}$$ [1]
（iii）Use your answer in（ii）to determine the period $$T$$ of the subsequent oscillation．
$$T=$$ $$\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots s$$ [3]
（iv）The experiment is repeated with an initial displacement of the trolley of $$2.4 \mathrm{~cm}$$．
State and explain the effect，if any，this change has on the period of the oscillation of the trolley．
Answer:
（i）$$F=k x$$ $$=8.0 \times(0.060-0.048)$$ or $$8.0 \times(0.060+0.048)$$ or $$8.0 \times 0.012$$ or $$8.0 \times 0.108$$
$$\Sigma F=(8.0 \times 0.012)-(8.0 \times 0.108)=0.77 N$$
or
$$\Sigma F=0.864-0.096=0.77 N$$
（ii）$$a=\frac{F}{m}$$
$$=\frac{0.77}{0.25}$$
$$=3.1 \mathrm{~ms}^{-2}$$
（iii）$$a=-\omega^{2} x$$
$$\omega=\sqrt{\frac{3.1}{0.048}}$$
$$\omega=8.04$$
$$T=2 \pi / \omega$$
$$\begin{aligned} \mathrm{T} &=2 \pi / 8.04 \\ &=0.78 \mathrm{~s} \end{aligned}$$
（iv）（resultant）force halved and distance halved
same $$\mathrm{T}$$
Explanation:
To solve this problem, let&
039;s break it down into steps:
Step 1: Calculate the Force on the Trolley at Release
- The spring constant, $$k$$, is given as $$8.0 \, \text{Nm}^{-1}$$.- The unstretched length of each spring is $$12.0 \, \text{cm}$$, and the stretched length in equilibrium is $$18.0 \, \text{cm}$$.
- The displacement from equilibrium when the trolley is released is $$4.8 \, \text{cm}$$.
Calculate the force exerted by each spring:
- The total extension of each spring when the trolley is displaced is $$18.0 \, \text{cm} + 4.8 \, \text{cm} = 22.8 \, \text{cm}$$.
- The force exerted by each spring is $$F = k \times \text{extension} = 8.0 \times (0.228 - 0.12) \, \text{m}$$.
Calculate the resultant force:
- The resultant force is the difference between the forces exerted by the two springs:
$$\Sigma F = 8.0 \times 0.108 - 8.0 \times 0.012 = 0.77 \, \text{N}$$.
Step 2: Calculate the Maximum Acceleration
- The mass of the trolley is $$250 \, \text{g} = 0.25 \, \text{kg}$$.- Use Newton&
039;s second law: $$a = \frac{F}{m} = \frac{0.77}{0.25} = 3.1 \, \text{ms}^{-2}$$.
Step 3: Determine the Period of Oscillation
- The angular frequency $$\omega$$ is related to acceleration and displacement: $$a = -\omega^2 x$$.- Calculate $$\omega$$: $$\omega = \sqrt{\frac{3.1}{0.048}} = 8.04 \, \text{rad/s}$$.
- The period $$T$$ is given by: $$T = \frac{2\pi}{\omega} = \frac{2\pi}{8.04} = 0.78 \, \text{s}$$.
Step 4: Effect of Changing Initial Displacement
- If the initial displacement is halved to $$2.4 \, \text{cm}$$, the force is also halved.- However, the period of oscillation $$T$$ remains the same because it is independent of amplitude for simple harmonic motion.
This detailed breakdown should help you understand the problem and the calculations involved.
3
Q&A
Basic
State what is meant by simple harmonic motion．[2]
Answer:
略
Explanation:
